Wärme trifft Mechanik.
Verbindendes und Aufbrechendes
Mechanik
Körper und auf ewig bestimmte Bahnen
Es gibt Körper, die sind ausgedehnt, undurchdringlich und räumlich begrenzt. Sind die Körper klein, nennt man sie Teilchen. So unterschiedlich diese Körper sind, eines haben sie gemeinsam: eine Masse, die angibt wie schwer oder wie träge sie sind. Die Körper oder Teilchen bewegen sich in der der Zeit im Raum. Innerhalb einer Zeitspanne bewegen sie sich eines Stücks Weges. Wirkt keine Kraft auf sie, dann fliegen sie mit der einmal eingenommenen Geschwindigkeit in die einmal eingenommene Richtung und Oritentierung in alle Ewigkeit weiter. Wirkt eine Kraft auf sie, dann werden sie gebremst oder beschleunigt. Sie ändern Geschwindigkeit, Richtung und eventuell die Orientierung.
Der Zustand eines Körpers wird durch seine Lage zu anderen Körpern ausgedrückt sowie dadurch, wie schnell sich seine Lage gegenüber anderen Körpern verändert. Dem Körper anhaftende Größe sind seine Masse und seine Ausdehnung, die beide durch Vergleich mit anderen Körpern bestimmt werden. Masse und Ausdehnung werden auf dieser Abstraktionsstufe als unveränderlich angenommen.
Beispiel Kanonenkugel

- Körper:
- Kanonenkugel mit Masse \(m\)
- Anfangsbedingungen:
- x-Richtung: Anfangsweg ist {0}, y-Richtung: Anfangs-Höhe \(h\)
- x-Richtung: Anfangs-Geschwindigkeit \(v\), y-Richtung: Anfangs-Geschwindigkeit \(0\)
- Beschleunigung in x-Richtung:
- keine Kraft, deshalb keine Beschleunigung \(\ddot {x}\Rightarrow m \cdot\ddot{x} = 0\)
- Beschleunigung in y-Richtung:
- zum Erdinnen Beschleunigung \(g \Rightarrow\) \( m\cdot \ddot{y} = - m \cdot g\)
- Geschwindigkeit in x-Richtung:
- \(\dot x = v\)
- Geschwindigkeit in y-Richtung:
- \(\dot {y} = -g\cdot t\)
- Weg in x-Richtung:
- \(x = v \cdot t\)
- Weg in y- Richtung:
- Der Weg ist \( h-y\). Mit \(y = -\frac{g}{2}\cdot t^2 + h\) ergibt sich für den Weg \(h-y = \frac{g}{2}\cdot t^2\)
Hinweise:
Für alle:
Orte sind \(x, y\), Geschwindikgkeiten werden mit einem Punkt \(\dot {x}, \dot{ y}\), Beschleunigungen mit zwei Punkten \(\ddot {x}, \ddot{ y}\) über dem Buchstaben geschrieben.
Für Rechkünstler:
\(\dot {x}, \dot{ y}\) und \(\ddot {x}, \ddot{ y}\) sind auch Rechenoperationen.
Für Neugierige
In \(m\cdot \ddot{y} = - m \cdot g\) haben die beiden Massen eine unterschiedliche Bedeutung. Das linke \(m\) ist eigentlich träge Masse \(m_t\) und das rechte \(m \) ist eigentlich schwere Masse \(m_s\) hervorgerufen durch Massenanziehung.
Die Newtonsche Theorie verlangt, dass beide Massen eine unterschiedliche Bedeutung haben. Erfahrung sagt, sie sind immer mit derselben Konstanten proportional. Das heißt man kann sie ihrem Wert nach gleich setzen. Wenn das nicht vor Unvernunft strotzt.
Wärme
Stoffe liefern und empfangen Wärme
Warme Stoffe liefern Wärme an kalte Stoffe, kalte Stoffe nehmen Wärme warmer Stoffe auf. Wenn Stoffe (im Modell ideale Gase) erwärmt werden (im Modell durch ein großes Wärmereserevoir) dehne sie sich aus, kühlt man sie ab, so ziehen sie sich zusammen. Sie ändern ihr Volumen (eine Größe für Ausdehnung, extensiv) und üben einen Druck (eine innere, intensive Größe unabhängig von der äußeren Form) beispielsweise auf einen beweglichen Stempel aus. Wie warm sie sind drücken wir durch eine ihnen innewohnende Größe, die Temperatur aus. Wärme ist proportional zur Masse (hier eine Mengengröße) eines Stoffes und zu seiner Temperatur. Dem Stoff innewohenende Größen sind spezifische Wärme und spezifische Masse.
Der Zustand eines Stoffes wird nicht durch Position und Ortsveränderung zu anderen Stoffen bestimmt. Er wird bestimmt durch seine Fähigkeit Wärme an andere Stoffe abzugeben oder von ihnen aufzunehmen, ob er das könnte (Wärmequalität) oder wieviel er könnte (Wärmemenge). Zur Untersuchung der Gesetzmäßigketen nimmt man auch Wärmesysteme, die von der Außenwelt isoliert sind. Anders als bei der reinen Mecahnik werden die meisten Gesetze dadruch gefunden, dass man Wärmesysteme mit der Außenwelt verbindet, idealereweise durch Mischen von Systemen oder durch Kontakt mit "unendlich" großen Wärmebehältern.
Beispiel: warme Flüssigkeiten mischen
2 gleiche Mengen Wasser werden zusammengeschüttet. Eine mit einer Temperartur von 100°C, die andere mit 60ºC. Im "Glas" ist dann die doppelte Menge mit einer Temperatur vo 80ºC.
 Die Mischung mit einer Temperatur von 80ºC ist ein experimentelles Ergebnis, das natürlich mit Reagenzgläsern wie oben nicht erzeilt werden kann. Bei der Mischung beider Mengen dürfen keine Wärmeverluste auftreten.
Die Mischung mit einer Temperatur von 80ºC ist ein experimentelles Ergebnis, das natürlich mit Reagenzgläsern wie oben nicht erzeilt werden kann. Bei der Mischung beider Mengen dürfen keine Wärmeverluste auftreten.
Bevor die Wärmemenge \(Q\) ihren Platz erhält, bleibt die Frage, was das dritte Reagenzglas mit dem 60ºC warmen Wasser symbolisieren soll. vor der Mischung hatten wir Wasser mit 100ºC, damit konnten wir Dinge desinfizieren. Nach der Mischung haben wir Wasser mit 80ºC. Damit können wir Wäsche waschen, aber nicht mehr desinfiziieren. Wenn wir jetzt die doppelte Menge 80ºC warmen Wassers mit der einfachen Menge 60ºC warmen Wassers mischen, erreichen wir irgendeine Temperatur unterhalb 80ºC und oberhalb 60ºC.
Durch noch so viel an warmem Wasser können wir die Wärmequalität von 100ºC warmen Wassers nicht wieder erreichen. Es geht Wärmequalität verloren, zerstreut. Die Wärmemenge ist geblieben.
Die Formeln
Die Mischversuche werden gut mit einer Wärmemenge \(Q\) beschrieben, die proportional zur Masse \(m\) des Stoffes ist und zur Temperatur \(T\). Die Konstante \(\eta\) wird addiert, weil Differenzen gemessen werden. die Proportinalitätskonstante \(c\) heißt spezifsche Wärme. Sie erweist sich als unterschiedlich für verschiedenen Stoffe.
$$ Q = c \cdot m \cdot (T+ \eta) $$Und jetzt für den Mischprozess
Jetzt nutzen wir die Formeln (das vermutete Naturgesetz). \(T_{80}\) ist nachher, also unbekannt.
$$ Q_{80} = Q_{100} + Q_{60} $$
$$ c \cdot 2\cdot m \cdot (T_{80} + \eta) = $$
$$ c\cdot m \cdot (100^{\circ} Celsius +\eta) + c\cdot m \cdot (60^{\circ} Celsius +\eta) $$
Hinweise
Für Rechenkünstler
Wer will kann die Mischtemperatur für dieselbe oder eine ähnlich Konstellation mit zwei Stoffen berchnen. Zum Beispiel Wasser und Nähmaschinenöl. K ist die Kelvintemperatur. \(T_{Kelvin} = T_{Celsius} + 273° \).
$$ c_{Wasser} = 4,186 ~ kJ/(kg·K) = 1,0 ~ kcal/(kg·K) $$
$$ c_{Öl} = 1,675 ~ kJ/(kg·K) = 0,4 ~ kcal/(kg·K) $$
Falls man Volumen will und nicht Massen, muss die spezifische Masse \(\rho\) verwendet werden.
$$ \rho_{Wasser} = 1 ~ g/cm3 $$
$$ \rho_{Öl} = 0,825 ~ g/cm3 $$
Für Neugierige
Wärmequalität gegenüber Entropie
Wärmequalität geht in die Wärme verloren, für die der Prozess nicht von innen heraus (ἐν (en) bedeutet „innen“) umgehrt werden kann (τροπή (tropē) bedeutet „Umkehr“ oder „Wende“). Diese "irreversible" Wärme heißt Entropie. Es gibt auch einen Begriff nahe bei Wärmequalität, nämlich Exergie.
Beispiel: ideale Gase
Wie auch in der Chemie wurden Gase häufig zur Erforschung von Wärmephänomenen und deren Zusammenhänge und Deutung gewählt. Wenn Gase sich mischen, kann die verloren gegangene hohe Temperatur wie bei Flüssigkeiten nicht wieder erreicht werden; es sei dann von außen wird erneut Gas mit höherer Temperatur zur Verfügung getellt.
Viele Gesetzte werden dadurch gefunden, dass Gase mit der Außenwelt in Kontakt sind und bleiben. Idealisiert wird die Außenwelt durch "unendlich" große Wärmebehälter einer bestimmten Temperatur, so das Verhalten idealer Gase
Gase mischen

Gase in wärmeisolierten Behältern. Die Wände werden entfernt und sie mischen sich. \(T_2 \le T_3 \le T_1\) wie bei der Mischung der Flüssigkeiten.
Verhalten idealer Gase - Druck, Volumen, Temperatur
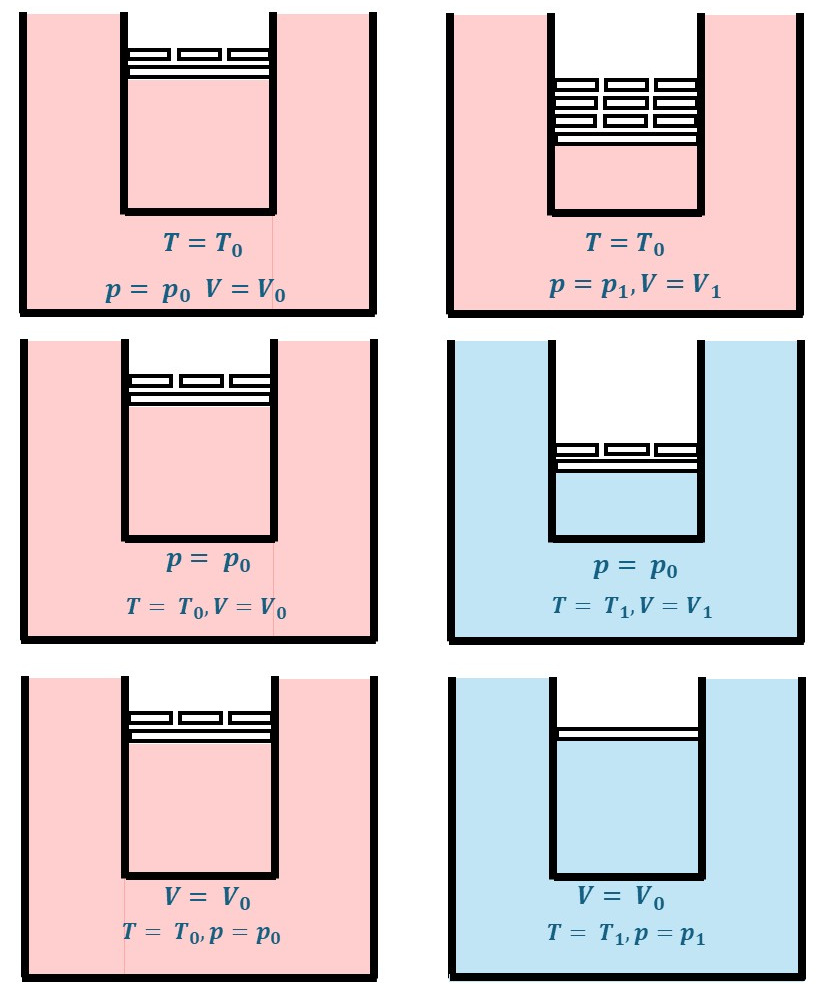
Lässt man eine von den 3 Zustandsgrößen konstant, so ändern sich die anderen. In den Bildern oben wird der Druck durch Gewichtsauflagen geändert, die Temperatur durch zwei Wärmereservoire unterschiedlicher Temperatur. Um das Volumen bei unterschiedlicher Temperatur konstant zu halten, werden Gewichtsscheiben entfernt.
Die Formeln
Für die Mischtemperatur gilt \(T_3 = \frac{T_1 + T_2}{ 2}\)
Das Gesetz für den Zusammenhang bei der Veränderung der Gaszustände lautet
$$p \cdot V = n \cdot R \cdot T$$
\(p, V, n, T\): Druck, Volument, Menge, Temperatur. \(R\) ist eine Konstante
Hinweise
Die Chemie hat gelernt, unterschiedlichen Stoffen auf den Stoff bezogene Massen zuzuordnen, die Atomgewichte oder die Molekulargewicht. Diesen Begriff "Molmassen" hat sie aus chemischen Experimenten gewonnen, wo eine bestimmte Menge Molmassen des einen Stoffes mit einer bestimmten Menge Molmassen des anderen Stoffes vollständige Verbindungen bilden.
Die Molmassen einiger idealer Gase:
| Wasserstoff | 2,016 (g/mol) |
| Helium | 4,0026 (g/mol) |
| Stickstoff | 28,0134 (g/mol) |
| Sauerstoff | 32,00 (g/mol) |
| Kohlendioxid | 44,01 (g/mol) |
| Methan | 16,04 (g/mol) |
| Argon | 39,948 (g/mol) |
Wenn also Wasserstoff von 2,016 g auf sein \( p, V, T \) - Verhalten untersucht wird, dann benimmt er sich genauso wie Helium von 4,0026 g oder Sauerstotoff von 32,00 g. Deshalb heißt \(R\) universelle Gaskonstante.
Für Neugierige
Wärmequalität gegenüber dem Verlust an Wärmequalität.
Wärmequalität geht meist in die Wärme niedrigerer Qualität verloren. Der seltene Prozess, der sich von "innen" heraus "umkehren" lässt, kennt keinen Verlust an Wärmequalität. Mit ἐν (en) („innen“) und τροπή (tropē) (Umkehr“ oder „Wende“) bennent Rudolf Clausius 1865 Entropie als Maß für den Verlust an Wärmequalität . Für den speziellen Prozess "inner Umkehr" (Entropie), ist der Verlust an Wärmequalität gleich 0. Sonst ist der Verlust größer als 0, dann liefert Entropie einen Wert größer als 0.
Es gibt auch einen Begriff nahe bei Wärmequalität, nämlich Exergie.
Energie
Energieumwandlung, mechanisch vollständig
Wärme , verwendet zum Garen, zum Schmelzen von Metall, zur Stoffumwandlung, zur Glasherstellung, zum Wohlfühlen, das ist eine ihrer seit Jahrhunderten genutzten Seiten. Eine weitere Seite findet sich in der Dampfmaschine. Sie wandelt Wärme in mechanische Arbeit um. Das Verbindunsglied ist Energie. Zu Lageenergie und Bewegungsenergie gesellt sich Wärmeenergie.
Mechanische Energie tritt als mechanische Arbeit und Bewegungsenergie auf. Innerhalb der Welt der Mechanik sind Arbeit und Bewegungsenergie vollständig ineinander umwandelbar. Was ich an Arbeitsfähigkeit gewinne, das verliere ich an Bewegungsenergie, was ich Arbeitsfähigkeit verliere gewinne ich an Bewegungsenergie. Nebenstehende Illustration vermittelt davon einen Eindruck. Es bleibt eine Frage, die die Mechanik nicht klären kann. Fällt ein Körper aus großer Höhe und bleibt am Boden liegen. Was ist dann mit dessen Bewegungsenergie geschehen?
Energieabgabe als Wärme
Es soll auf einmal die beim Heben aufgewendete Energie nach dem Fall verschwunden sein? Die vollständige Umwandlung ist eine Abstraktion, näherungsweise tauglich aber unvollständig.
Wenn ein Körper seine Energie an "den Boden" verliert, ist nicht ersichtlich, dass der Boden sich erwärmt hat. Beobachtungen bei Bearbeitung von Kanonenrohren helfen weiter . Rohre einigermaßen rund zu drehen war noch manuell erfahrbare Arbeit. Bearbeitung erwärmte, besser erhitzte diese Rohre. Mechanische Arbeit wandelt sich in Wärme.
Umwandlung von mechanischer Energie in Reibungswärme
Benjamin Thomson (1798), Robert Mayer (1842) haben den Gedanken in die Welt gesetzt, dass Wärme auch eine Form von Energie – damals Kraft genannt – ist. James Joule (1850) bestimmte in präzisen Messungen das "Mechanische Wärmeäquivalent".
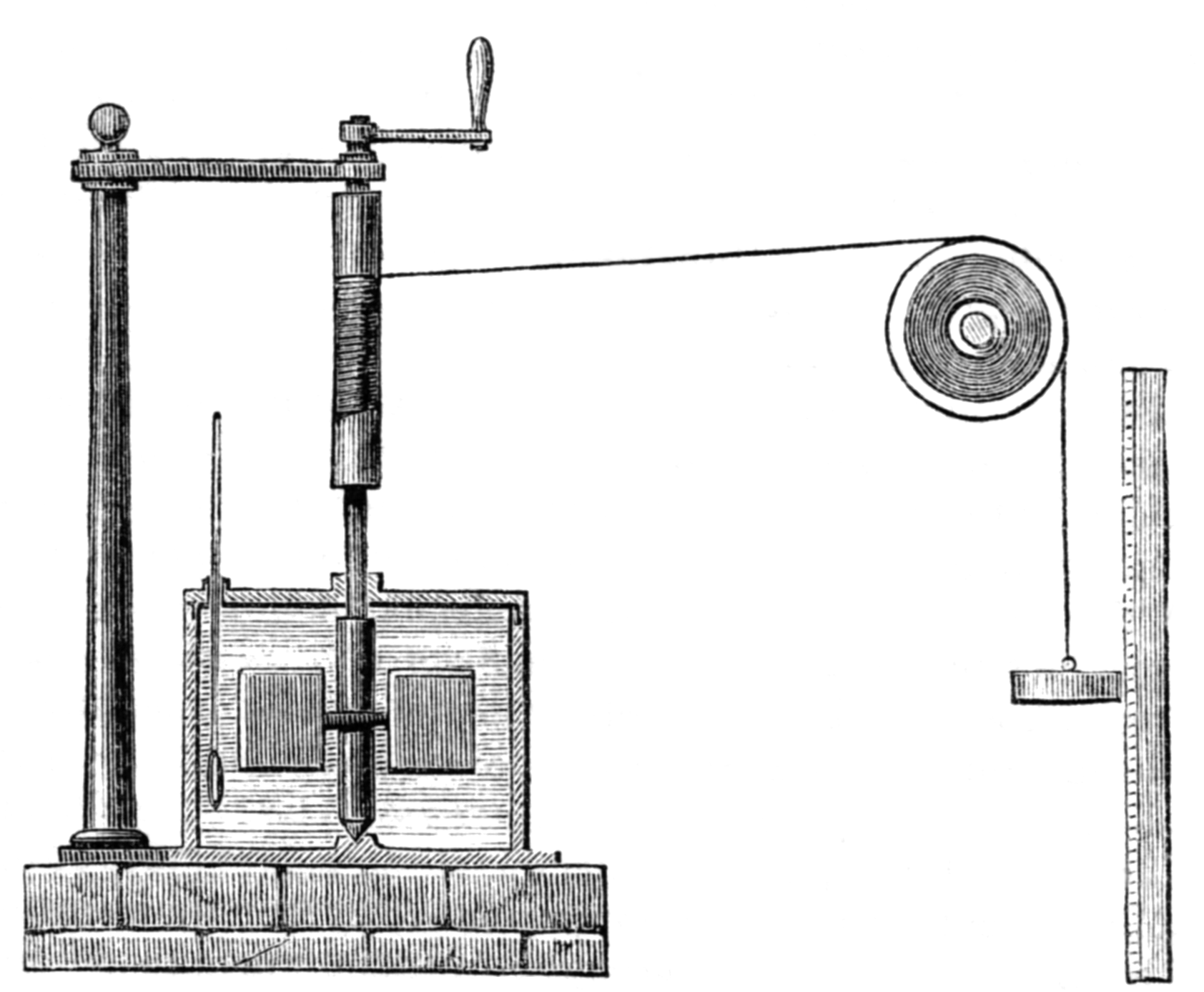
Apparat, mit dem Joule das mechanische Wärmeäquivalent gemessen hat.
Joule fasst nach Wikipedia seine Ergebnisse so zusammen: „[…] daſs die Wärmemenge, welche im Stande ist ein Pfund Wasser (gewogen in Vacuo und genommen zwischen 55 und 60° F.) in seiner Temperatur um 1° F. zu erhöhen, zu seiner Erregung den Aufwand einer mechanischen Kraft erfordert, die durch den Fall von 772 Pfund durch einen Raum von einem Fuſs vorgestellt wird.“
Dies bedeutet in heutigen Maßen: 1 kcal15 ≙ 423,6 kp·m = 4,154 kJ.
Beispiel Reibschweißen
Schweißen mit Hitze durch Reibung erzeugt
Für Rechenkünstler
Ritt durch physikalische Einheiten
- 1 Kalorie (cal) ist die Menge an Wärme, die benötigt wird, um 1 Gramm Wasser um 1 Grad Celsius zu erwärmen.
- Die Umrechnung der Temperaturerhöhung ergibt \(\Delta T = 1^\circ F= \frac{5}{9}^\circ C\)
- Ein Pfund (lb) entspricht 453,59 Gramm (g).
Die Erwärmung von 453,59 g Wasser um 1ºF oder 5/9 ºC entspricht also 252 cal.
- 1 Fuss (ft) entspricht 30,48 cm = 0,3048 m.
- 772 lb entsprechen \(772~lb \cdot 453,59~g/ft \approx 350171,5~g \approx 350,172~kg\).
- Die Gewichtskraft ist \(F_g = 9,81~m/sec^2 \cdot 350,172~kg \approx~3435~N \)
Die Energie, die in Wärme verwandelt wurde ist der Verlust an potentieller Energie, der Gewichtskraft mal der verlorenen Höhe.
Die in Wärme umgewandelts Energie beträgt 3435 N mal 0,3048 m, als ungefähr 1047 Nm.
$$1 cal \approx 4,16~Nm = 4,16~J$$
Hinweis auf Quellen
- Quelle Reibschweißen: https://de.wikipedia.org/wiki/Datei: Schwungradreibschweissen.ogv
- Quelle Joules Appart: Joule's Apparatus (Harper's Scan) - Wärmeäquivalent – Wikipedia
- Quelle Drehen: 1280px-Nasmyth_Lathe.png (1280×890)
Ein Artikel in Wikipedia erzählt die Geschichte, wie Mechanische Energie in Reibungswärme verwandelt wird.
Physikalische Arbeit und Wärme
Im 17-ten und 18-ten Jahrhundert haben Heerscharen von Tüftlern danach gesucht, physikalische Arbeit aus dem Nichts zu gewinnen – für das Heben von Lasten, für das Pflügen des Ackers, für das Mahlen von Korn, für die all die beschwerlichen Dinge des Lebens .
Die Brücke von Mechanik zu Wärme erweist sich als höchst ungerecht. Abstrakt bleibt mechanische Bewegung ewig. In der Wirklichkeit wandelt sie sich zu einem kleinen oder großen Teil immer in Wärme. Diese Wärme kann nicht vollständig als mechanische Arbeit zurückgewonnen werden. Ich weiß nicht, wie es anderen geht, aber den oben angesprochenen Tüftlern ging das gegen den Strich, besser – wie es schien, war es wider die Vernunft. Zwar ist es ist eine von vielen Menschen sinnlich wahrgenommene Tatsache, dass Wärme nicht beliebig in Arbeit verwandelt werden kann, dennoch ist es eine Tatsache, die nicht allgemein als Naturgesetz aktzeptiert wurde.
"Gott" sei Dank, wenigstens ein Teil von Wärme kann in mechanische Arbeit verwandelt werden. Der andere Teil eben nicht. Er ist für Mechaniker der Arbeit vergeudet. Diese Vergeudung oder Abnhame der Wärmequalität kann nicht rückgängig gemacht werden.
Man kann in "reversiblen" Prozessen die Wäremequalität halten. Immerhin und zum Beispiel in einem isothermen Prozess mit Volumenarbeit.
Volumenarbeit an idealem Gas
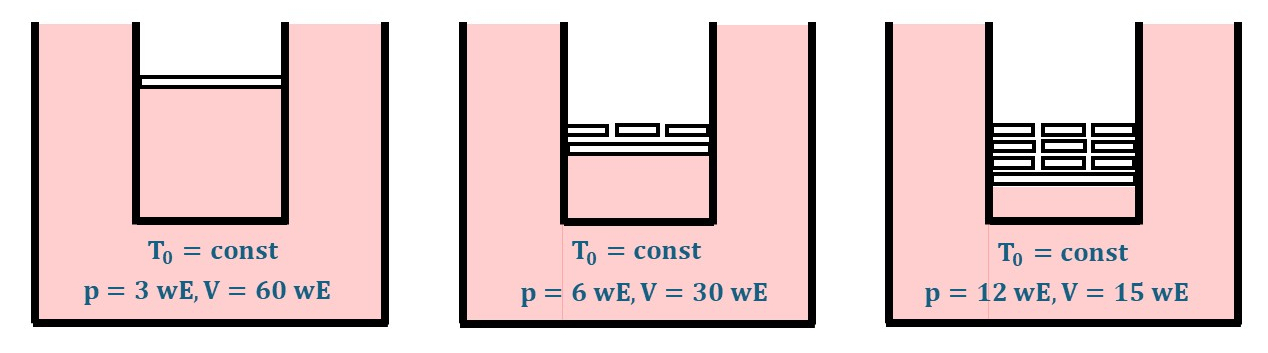
Über den Wärmeaustausch mit einer großen Umgebung wird die Temperatur eines Gases konstant gehalten. Das Gas befindet sich in einem Zylinder mit Deckel, es kann kein Gas entweichen. Durch Zugabe von Gewichten auf den Zylinderdeckel wird es komprimiert, wie die nächste Grafik zeigt.
Was sind wE? Natürlich misst man Druck und Volumen mit physikalischen Einheiten (s.Hinweise). Um das ideale Gasgesetz anschaulich mit Gewichtsscheiben darzustellen genügen hier wE: willkürliche Einheiten.
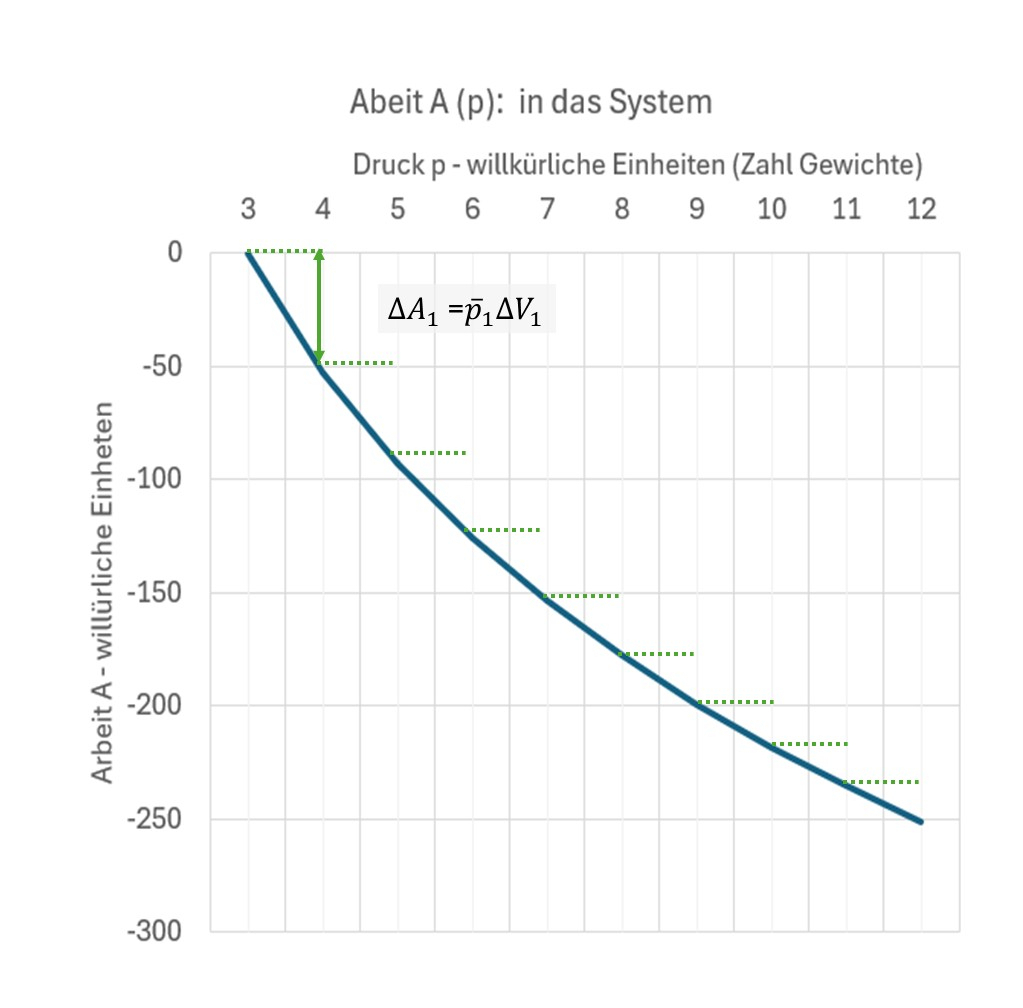
Legt man auf den Deckel ein kleines Gewicht \(\Delta F_g\) zusätzlich zu dem schon darauf liegendem Gewicht, so sinkt der Deckel um einen Weg \(\Delta s\). Dadurch wird Arbeit am Gas verrichtet. Sie ist: \((F_g + \Delta F_g) \cdot \Delta s\). Mehrmals ein kleines Gewicht aufgelegt, wird Arbeit verrichtet als \(A = \sum_{i=1}^n~\Delta A_i\).
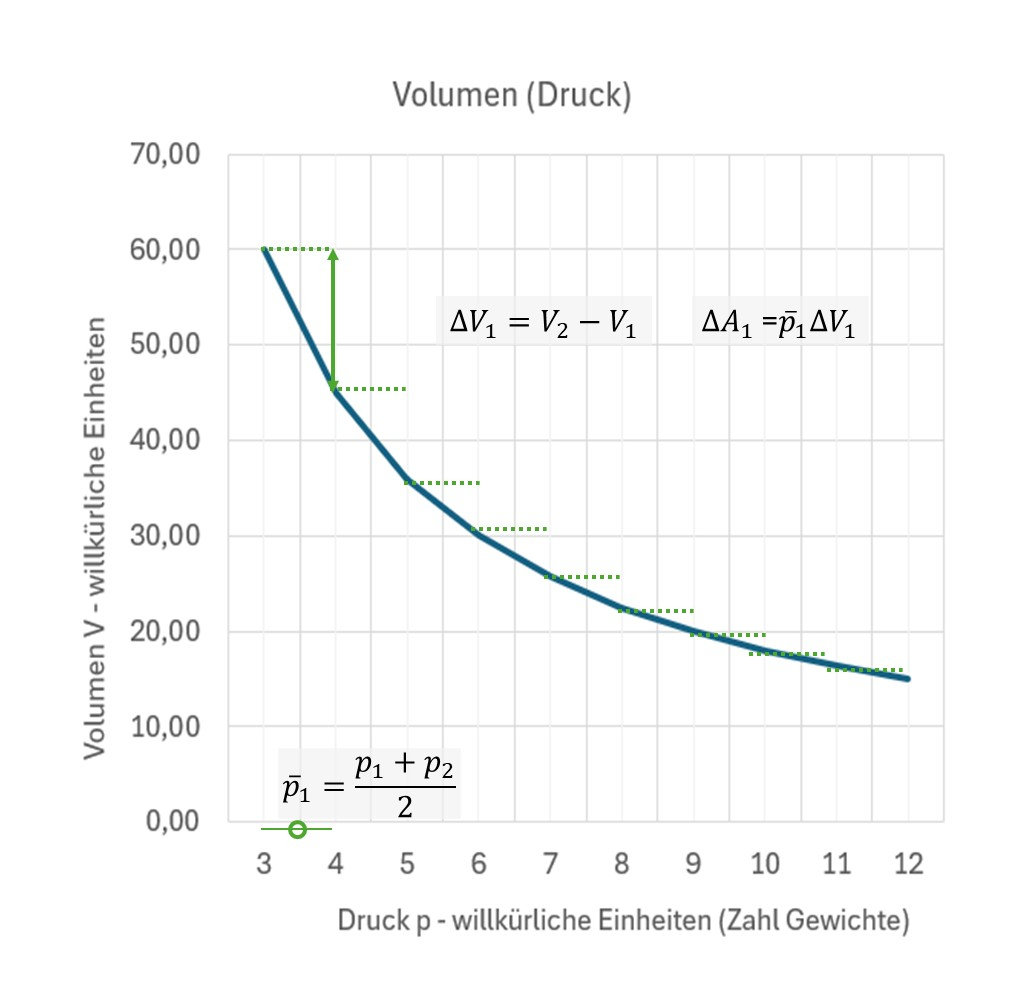
Das Volumen fällt mit dem Druck. Weil endliche Intervalle gewählt wurden, wird ein mittlerer Druck angenommen.
Es werden kleine Arbeitselemente aufsummiert zu einer bis zu einem Druck erfolgten Arbeitszufuhr.
Für Neugierige
Man kann den ganzen Prozess umkehren. Durch die Volumenarbeit wurde dem Gas Wärme zugeführt, die in die Wärmereservoirs abgegeben wurde. Nimmt man die Gewichte Schritt für Schritt wieder vom Deckel, so expandiert das Gas. Die Wärmereservoirs geben Wärme an das Gas, so dass die Temperatur konstant bleibt. Diese Wärme wird jetzt als Arbeit nach außen abgegeben.
Führt man beide Teile des Prozesses hintereinander durch, so wird weder Arbeit noch Wärme im Gesamtprozess erzeugt. Solch einen Prozess nennt man reversibel.
Hinweise
Kraft und Druck
Die Gewichte – insgesamt \(F_g\) – auf dem Deckel das Zylinders üben einen Druck auf das Gas aus. Sie liegen auf einer Deckelfläche \(A_{Deckel}\). Der Druck ist dann \(\frac {F_g}{A_{Deckel}}\) (A ist in diesem Fall ein Fläche).
Volumen
Wenn der Deckel sich um einen Weg \(\Delta s\) bewegt, dann ändert sich das Volumen. \(\Delta V = \frac {F_g}{A_{Deckel}} \cdot \Delta s\). Damit wird \(\Delta A_i = p_i \cdot \Delta V_i\).
Maßeinheiten
Der Druck wird gemessen in Pascal \(1~Pa = 1~\frac {N}{m^2}\), das Volumen in \(m^3\).
Zur Orientierung: Der Luftdruck beträgt \(1~atm≈1~bar=101~325~Pa\). Der Druck \(p\) durch die Gewichte \(F_g\) auf das Gas über den Deckel der Fläche \(A_{Deckel}\) ist \(p = \frac{F_g}{A_{Deckel}}\).
Mechanische Energie kann sich in Wärmeenergie umwandeln. Auch kann man die Wärmequalität erhalten, Arbeit und Wärme austauschen. Aber in Wärme vergeudete Arbeit und vergeudete Wärme bleibt vergeudet. Man kann mit Chemie und mechanischer Arbeit in einem System die Wärmequalität (seine Temperatur) erhöhen, zu dem Preis in einem darum liegenden System Wärmequalität zu entziehen.
Ein Maß für den Verlust an Wärmequalität. Entropie.
Rudolf Clausis formulierte 1850, dass Wärme nur vom warmen zum kälteren Körper fließen kann . Er fand auch ein Maß, dass die Differenz zwischen den Zuständen Warm und Kälter – oder zwischen höherer und niedrigerer Wärmequalität – angibt. Dieses nannte er Entropie \(S\), in diesem Text heißt es häufig Verlust an Wärmequalität. Wärme \(Q\) selbst ist keine gutes Maß, weil sie davon abhängt, wie man von einem Wärmezustand zum anderen kommt. Es zeigt sich aber, dass eine Größe \(\frac{Q}{T}\) nur vom Wärmeanfangs und -endzustand abhängt.
Wärme ist kein Zustand
Wenn man die Wärmebilanz zweier Prozesswege betrachtet, so hängt sie vom Prozessweg ab. Es zeigt sich aber, dass man eine Größe gewinnen kann, die davon unabhängig ist. Sie heißt Entropie.
Ein Beispiel mit zwei Prozesswegen.
Wir beginnen mit demselben Verfahren a wie bei "Volumenarbeit am idealen Gas", gehen aber einen weiteren Prozessweg b mit denselben Anfangs- und Endzuständen von Temperatur, Volumen und Druck. Die Temperatur wird jeweils durch eine unendlich großes Wärmebad geregelt.
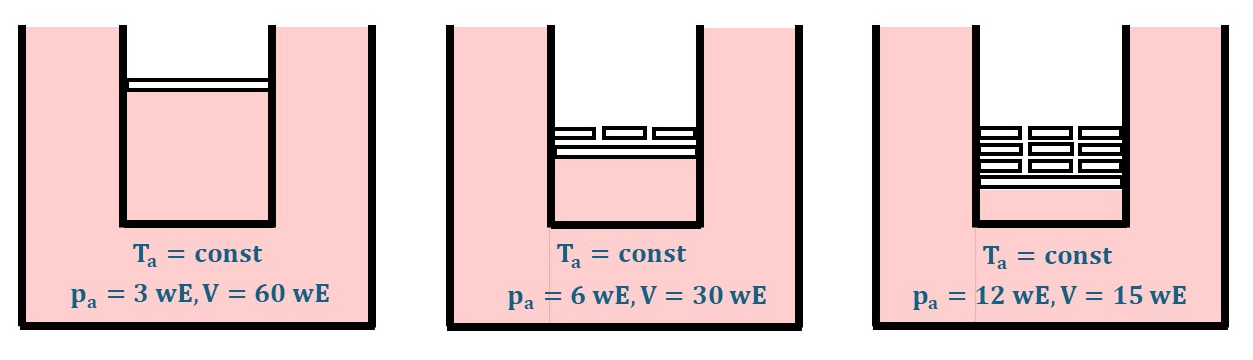
Kompressionsarbeit \(W_a\) gibt Wärme \(\Delta Q_a\) in das System Zylinder und Wärmebehälter.
Hinweis: Für das Schema genügen "willkürliche Einheiten" \(wE\).
Anfangszustand:
$$ T_a, V = 60~wE, p_a =3~wE $$
Kompression bei konstanter Temperatur \(T_a\)
Endzustand:
$$ T_a, V = 15~wE, p_a =12~wE $$
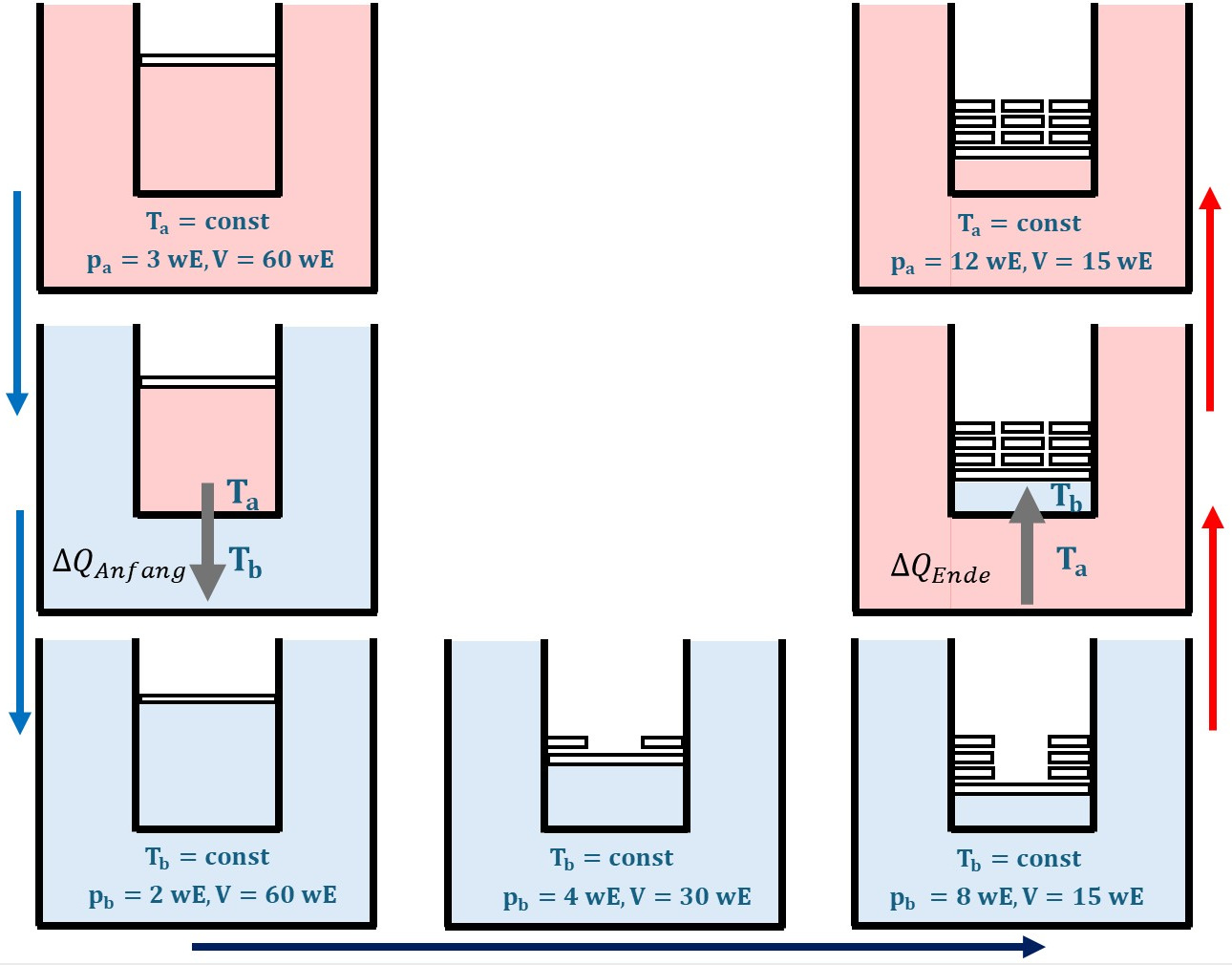
Kompressionsarbeit \(W_b\) gibt Wärme \(\Delta Q_b\) in das System Zylinder und Wärmebehälter.
Anfangszustand:
$$T_a, V = 60~wE, p_a =3~wE$$
Abkühlen des Gases auf \(T_b\), Anpassung des Volumens \(V\) auf dasselbe wie in a durch Senkung des Drucks auf \(p_b\).
Kompression bei konstanter Temperatur \(T_b\)
Aufwärmen des Gases auf \(T_a\), Anpassung des Volumens \(V\) auf dasselbe wie in a durch Vergrößerungs des Drucks auf \(p_a\).
Endzustand:
$$T_a, V=15~wE, p_a =12~wE$$
Man beachte:
\(\Delta Q_{Anfang} + \Delta Q_{Ende} = 0\)
Mit dem Verfahren von "Volumenarbeit bei idealen Gasen" ist die Kompressionsarbeit und von a:
$$ \Delta Q_a = W_a = \sum_{i=1}^n p_i\cdot \Delta V_i = M\cdot R\cdot T_a\cdot \sum_{i=1}^n \frac{\Delta V_i}{V_i}$$
und die von b:
$$ \Delta Q_b = W_b = \sum_{i=1}^n p_i\cdot \Delta V_i = M \cdot R\cdot T_b\cdot \sum_{i=1}^n \frac{\Delta V_i}{V_i}$$
Die Summenterm ist in beiden Fällen gleich. Aber der Faktor vor der Summe unterscheidet sich. Obwohl in beiden Fällen die Anfangs- und die Endzustände gleich sind ändert sich der Wärmeinhalt des Endzustandes.
$$ Q_{a-Ende} = Q_{Anfang} + \Delta Q_a \neq Q_{Anfang} + \Delta Q_b = Q_{b-Ende}$$
Wärme definiert keinen Zustand, der unabhängig vom Prozessweg erreicht wird.
Die durch die Temperatur geteilte oder reduzierte Wärme ist gleich:
$$ \frac {\Delta Q_a}{T_a} = \frac {\Delta Q_b}{T_b} = \Delta S $$
oder
$$ S_{a-Ende} = S_{b-Ende}=S_{Anfang}+ \Delta S $$
\(S\) heißt Entropie, bei einigen einfach Wärme oder hier häufig Maß für den Verlust an Wärmequalität.
Für Neugierige
Wer genau hinguckt merkt, dass \( \Delta S = M\cdot R\cdot \sum_{i=1}^n \frac{\Delta V_i}{V_i}\) negativ wird. Das liegt daran, dass das nächste Volumen immer kleiner ist als das vorherige, \(V_{i+1} - V_i = \Delta V_i <0\), also negativ. Ein negativer Verlust an Wärmequalität oder eine Erhöhung der Wärmequalität? Die bisherige Erzählung scheint nicht zu stimmen, Wäremqualität ginge in der Tendenz verloren.
Scheint nur. Es wurde mechanische Arbeit in das System gesteckt. Führt man den Prozess anders herum, vom kleinen zum großen Volumen, so wird die Änderung der Entropie \(\Delta S\) positiv mit demselben Betrag.
$$ \Delta S_{total} = \Delta S_{hin} + \Delta S_{zurück}= 0 $$
In diesem Fall liegt ein "reversibler" Prozess vor. Es ist aber keine Arbeit gewonnen. Es bleibt dabei \(\Delta S \geq 0\).
Für Rechenkünstler
$$ \Delta S = M\cdot R \cdot \sum_{i=1}^n \frac{\Delta V_i}{V_i} \approx M\cdot R \cdot \int_{V_{Anfang}}^{V_{Ende}}\frac{dV}{V} = M\cdot R \cdot ln \frac{V_{Ende}}{V_{AnFang}} $$
Hinweis
\(R = 8,314 \frac {J}{mol \cdot K} = 1,987 \frac{cal}{mol \cdot K}\) heißt ideale Gaskonstante, \(M\) ist eine Menge, die Anzahl molarer Massen. \(J\) und \(cal\) sind die Energiemaße Joule und Kalorien. \(K\) ist das Maß für die absolute Temperatur, Grad Kelvin oder einfach Kelvin.
Mischentropie Wasser
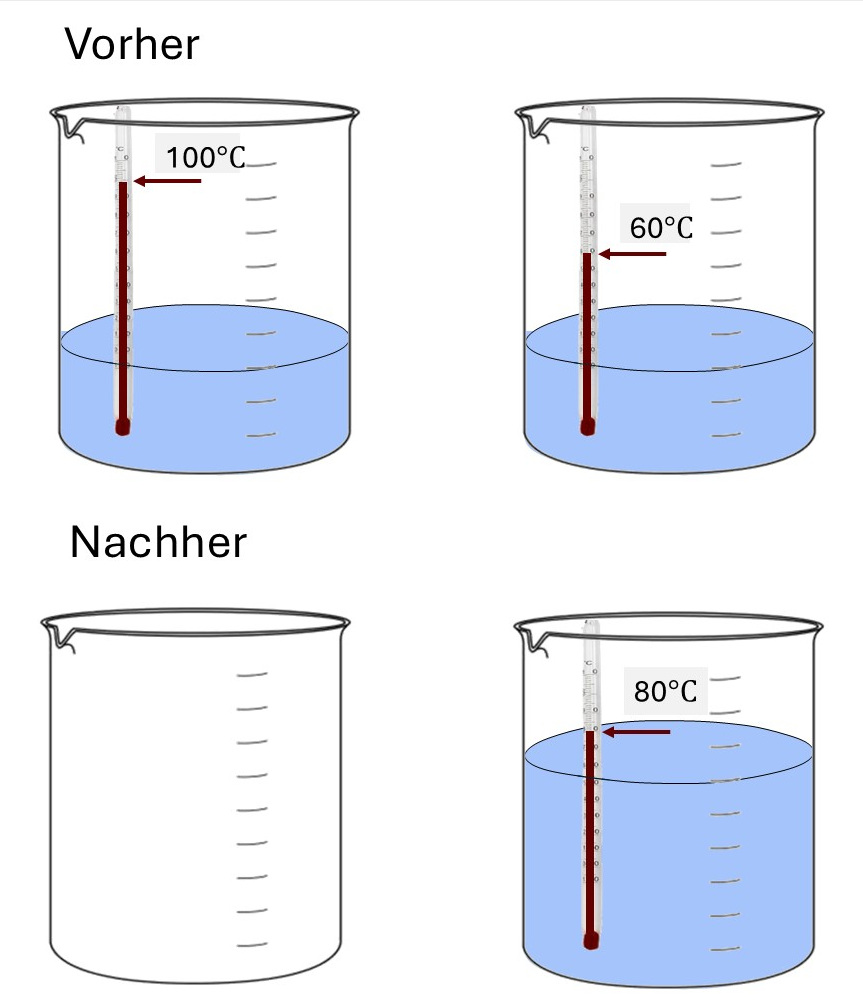
Mischung von Wasser gleicher Masse und unterschiedlicher Temperatur
Wie stellen wir uns den Mischprozess vor? Wir schütten das Wasser zusammen und warten auf den Temperaturausgleich. Das ist kein langsamer Prozess, bei dem kleine Schritte immer wieder zum Gleichgewicht führen. Also geben wir langsam das eine Wasser in das andere Wasser \((\Delta m\), \( \Delta T\)). Oder wir führen einen langsamen Temperaturausgleich durch Kontakt zwischen den beiden Flüssigkeiten her (\(\Delta T\)). Letzteren Prozess nehmen wir. Wir wissen ja, dass die Entropieänderung vom Prozessweg unabhängig ist.
$$ \Delta S = \sum_{T_{\text{start}}}^{T_{\text{end}}} \frac{\Delta Q_{\text{rev}}}{T} = mc \sum_{T_{\text{start}}}^{T_{\text{end}}} \frac{\Delta T}{T}$$
$$\Delta S_{T-hoch} + \Delta S_{T-niedrig} = 0$$
Weiter wissen wir dass, bei gleichen Massen \(m\) für die Mischtemperatur gilt:
$$T_{Mischung} = \frac {T_{hoch} + T_{niedrig}}{2}$$
Die Summen kann man zum Beispiel für 10 Schritte mit Excel berechnen. Wir sind Rechenkünstler und berechnen dort.
Expandierendes Gas
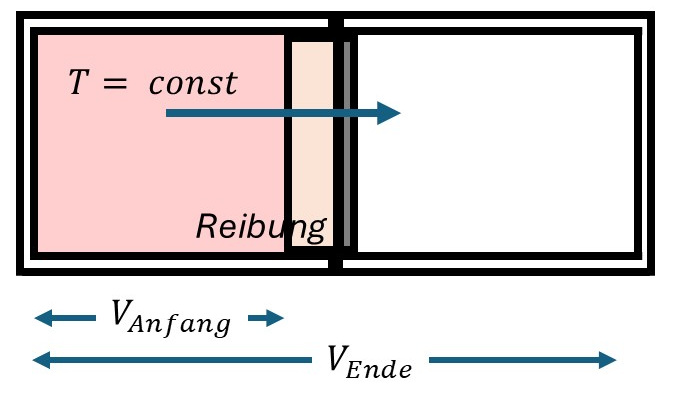
Gas expandiert kontrolliert ins Vakuum. Die Expansionsarbeit wird in Reibung des angedeuteten Stempels verwandelt.
Ein Gas ist in einer Hälfte eines Kastens eingesperrt. In der anderen Hälfte herrscht Vakuum. Das Gas möge vollständig und bei konstanter Temperatur einen Stempel in die Vakumhälfte drücken. Die konstate Temperatur wird zum Beispiel dadurch erreicht, dass der Stempel an der Wand reibt. Das macht ihn langsam und die Reibungswärme aus Expansionsarbeit hält die Temperatur konstant.
$$W= \sum_{i=1}^n p_i \cdot \Delta V_i = \cdot M \cdot R \cdot T \cdot \sum_{i=1}^n \frac {\Delta V_i}{V_i} $$
Die Berechnung erfolgt unter "Für Rechenkünstler".
Für Rechkünstler:
Mischung
Die Entropie ändert sich im Modell konstanter Masse (die Temperatur gleicht sich vor dem Mischen an) für jede Einheit:
$$\Delta S = \int_{T_{\text{start}}}^{T_{\text{end}}} \frac{\delta Q_{\text{rev}}}{T} = mc \int_{T_{\text{start}}}^{T_{\text{end}}} \frac{dT}{T} = mc \ln \left( \frac{T_{\text{end}}}{T_{\text{start}}} \right)$$
Die Summe ist:
$$\Delta S_{gesamt} = mc \left(\ln \left( \frac{T_{\text{end}}}{T_{hoch}}\right) + \ln \left( \frac{T_{\text{end}}}{T_{niedrig}} \right)\right)$$
Expansion
$$W= MRT \cdot \int_{V_{Anfang}}^{V_{Ende}} \frac {dV} {V} = MRT \cdot ((ln (V_{Ende})- ln (V_{Anfang})) = MRT \cdot ln (\frac {V_{Ende}} {V_{Anfang}})$$
$$\Delta S = MR \cdot ln (\frac {V_{Ende}} {V_{Anfang}})$$
Unter speziellen Bedingungen kann die Entropiedifferenz (der Wärmeverlust) \(\Delta S\) allenfalls \(0\) werden. Sonst gilt, dass sie oder der Verlust an Wärmequalität zunimmt, \(\Delta S \gt 0\).
Fazit
Die ewige Bahn der Planeten, die stabile Schönheit des Himmels geht dahin. Dafür haben wir uns die Dampfmaschine und die große Industrie geschenkt. "Gott" ist groß und das Weltall auch. Jenseits der klassischen Mechanik und des klassichen Wärmeverständnisses gibt es Chaos, dass Ordnung schafft. Ein Schritt dahin liefert uns die statische Mechanik, in der sich unendliche und deterministsiche Mechanik wie die schnöde, endliche, mit Zerfall und Zufall behaftete Wärme aufheben.
Wärme wird meist direkt (chemisch) durch Verbrennen erzeugt, häufig aber auch aus Elektrizität, die wiederum durch mechanische Arbeit, die wiederum ...
Wärme und Hitze werden zur Erzeugung von Wasserdampf genutzt. Der Dampfdruck erzeugt mechanische Arbeit.
Um 1800 herum wurde der Drehmeissel noch mit Muskelkraft gegen das Werkstück gepresst. Thomsons Entdeckung der Reibungswärme an Kanonenrohren erfolgte 1798. Ab 1840 setzten die Dreher einen Schlitten mit dem Drehmeißel ein.
.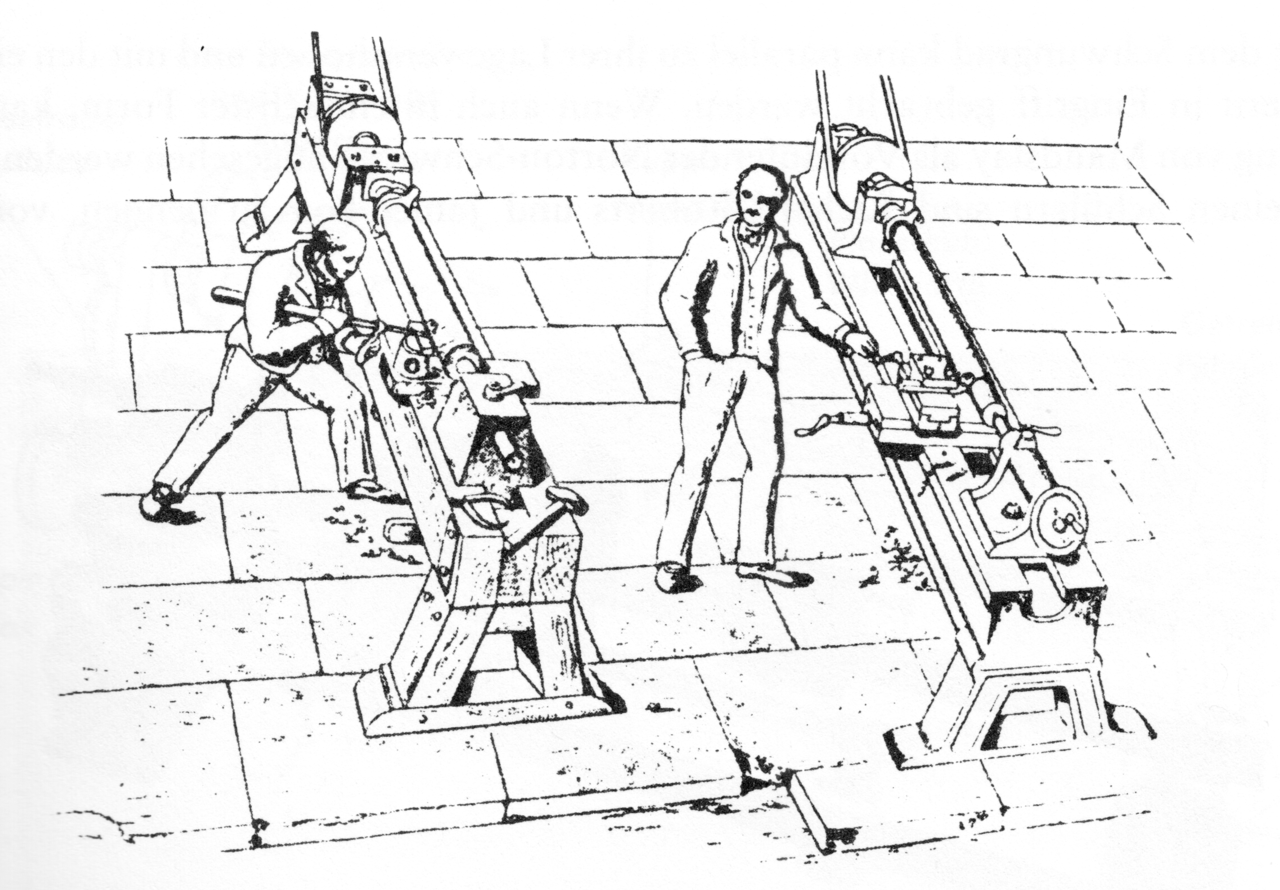
Manuelles Drehen links, Drehen mit Schlitten rechts.
Der Glaube an das Perpetuum Mobile hat Generationen von Tüftlern verrückt gemacht.
Wikipedia zu dem schillernden Begriff Entropie